Say you’re building a database… #

…like it’s a normal thing or something. Eventually you’ll need to store the data on disk.

That’s not too much to ask, is it?

Storage requirements for database servers are not that extreme. It just needs to be

• Fast
• Cheap
• Compact
• Durable
• Secure
• Reliable
• Horizontally scalable
• Vertically scalable
• Smell good
• Come in a variety of flavors and colors

How hard can it be?

It should, then, come as no surprise that I chose to ignore all that and instead just try figure something that can be built by a single person and still function.

But I still want it to smell good. That’s an important functional requirement.

Searching the Internet for “Which file format smells the best” didn’t return anything useful on the first page, so I had to go and read a bunch of papers about how SSDs work, various database structures and how they interact with transaction state, recovery and so on.

You know, the standard research methodology.

I decided to use a log structured merge tree not just because it’s a cool name, but also because I quickly realized that I can skip the “merge” and “tree” parts and still have a cool sounding LS-store, which is a fancy way of saying “append bytes to an array without any real structure”, but all scientific and stuff.

And then I built it. This post is the first of many about how Glowdust’s LSM tree implementation works as it is being developed.

Skip directly to the end if you’re here just for the smell reviews¹.

Basic design #

If we think of Glowdust function mappings as key/value pairs, then the store needs to do two things:

• Given a function argument (i.e. a key), find the corresponding value if it exists
• Iterate over all key/value pairs for a function

These correspond to the two operators the planner knows about at time of writing. As more operators are introduced (range scans, index based filters and so on), more features will be required, which will be supported by either the store or auxiliary structures (like indexes).

But that’s not all!!!

LSM implementations generally keep transaction state in memory as an efficiently indexed structure (e.g. skip list) that allows for quick lookups and for fast merge phases. When the transaction commits, the memory state is converted into the first tier of the merge tree by sorting and removing duplicates. That same first tier can also be used as the write ahead log, to enable recovery.

I had a slightly different idea. I want to keep memory allocations as close to zero as possible, which for the transaction state means using the page cache directly. This opens up some interesting behaviors that I want to explore, but I won’t go into details in this post.

And we also need to think about transaction management. You know, the thing that separates the wheat from the chaff of database implementations.

I find it very elegant to keep every ongoing transaction as a collection of pages in the page cache. I can then spill them to disk, move them around processes, and commit them just by flipping a bit somewhere and making them public. It also lets me dynamically balance memory use between transaction state and file buffers without the user having to care about it.

Keeping everything in the page cache means basically keeping everything in a file, which in turns means no pointers, just offsets. This isn’t a big deal in theory, but in practice it can lead to complicated code, mostly because all memory management needs to happen in the file itself - managing memory and using memory is the same thing, there is no allocator running in the background.

To compensate for that, and let a single person manage the complexity, things need to remain simple. And for disk operations, simple means append only.

So I did that.

Ordered memtable #

The current LS store doesn’t do merges - in fact, at time of writing it doesn’t even serialize to disk.

It doesn’t need to, really. The merging step is just glorified optimization, because the system can always read the store from the memtables.

And persistence is necessary if you run out of memory or want durability. Glowdust is not there yet.

So memtables only. Fine.

Why ordered memtables? Mostly for convenience, less for performance, although I expect this to change soon. Keys are looked up all the time, and doing so in order is just faster².

Special mention is necessary for the “log” part of the Log Structured store. In essence it means that entries are not updated in place (well, mostly). We can only append. Under this constraint, updates and deletes do not modify existing data in place - instead, we append the updated value and we tombstone the old one, by updating a flag, forwarding with a pointer or something of that nature.

This also plays nicely with SSDs, which physically really, really dislike writing partial blocks.

A memtable is made of Entries #

So here’s the structure of the ordered memtable, starting with a single Entry:

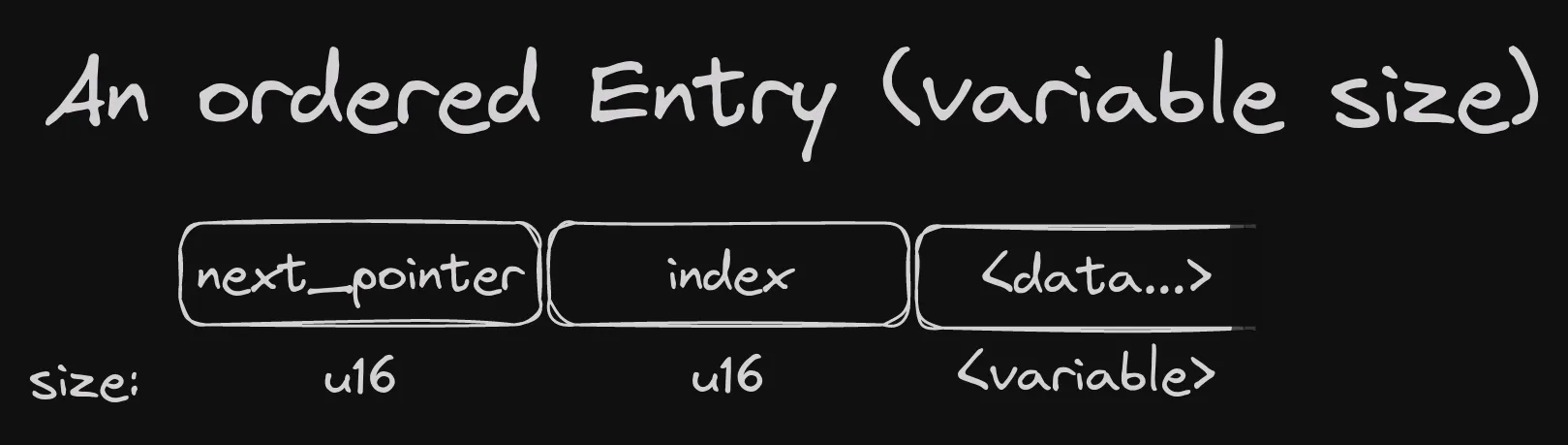
The next_pointer field is a linked list pointer, pointing to the next largest entry. The twist, of sorts, is that it points to the next entry that is actually in use, skipping tombstoned entries (we’ll see this in more detail later).

The index field plays two roles. The first is straightforward - it keeps the index of the entry. When we scan the memtable in entry order, we jump around positions, which that for every entry we land on, we don’t know its index in the list. This field keeps that.

The second role is that if an entry is updated, the old version needs to be marked as not in use, so that linear scans of the memtable can skip it. Setting the index field to u16::MAX_VALUE does the trick.

Finally, the data field is variable in size, but that’s not a problem, because serialized values need to know how to read and write themselves, and report the size when they do. The memtable only needs to know the length when scanning through entries.

Many Entries make a memtable #

Many entries together, linked as a list make up a memtable. We just need a few more fields to maintain the structure. Here’s what that looks like:

Remember when I said that I want this to be in the page cache? This means there is nothing “in memory” for the memtable. The whole thing needs to be serialized to disk and be wholly self contained and readable once read back. Hence, we need fields to keep track of things. The first is the smallest_value_offset, the pointer to the smallest value in the memtable, i.e. the start of the linked list. This is updated every time we add an entry to the head of the list.

The second is the write_position, the offset in the array that the next entry will be written to. This value is updated with every entry written.

Finally we have the value count - the number of entries written so far. This is incremented for every value added.

The memtable has another trick up its sleeve. From the end of the file and growing towards the start there are u16 fields that I call “index pointers”. These are pointers to the corresponding entry, meaning that the first index pointer, the one at the largest offset, points to the first entry, the second index pointer points to the second entry and so on. This allows for direct index lookups of entries without requiring a scan.³. To find index entry #n, just multiply n by the size of u16, go to that offset from the end of the array and read a u16. That’s the offset of entry #n. Index pointers are quite straightforward, so I won’t bother with them any more, just to point out that we know exactly where the next pointer should be written, because we know the value_count: It’s always value_count * size_of(u16) from the end of the array.

Reading data #

Ok, we got all our bytes in order. How do we read entries?

The main use for a memtable is to translate a value to an index, which sounds kind of underwhelming when I write it out like this, but there you have it.

So, how to do that?

There are two ways, actually. One is by linear scan, the other by searching in order.

Searching linearly #

This is the most straightforward case. We know the size of each value (well, the value knows it, the memtable just cares that it can be discovered), so we can start at the beginning and read each entry in turn, skipping those that are tombstoned.

We need to keep an offset to the current entry, of course, and that is updated with the length of every entry read. Once that offset is larger than the write_position, we know we’ve exhausted the memtable and the key was not found.

Searching in order #

Similar as above, except that the next entry to read is determined by the next_pointer field of the current entry. Tombstone checks aren’t needed, since (as we’ll see in the Updates section) when updating a value the next pointer always points to the latest version.

Inserting new keys #

Insertion is no more complicated than maintaining an ordered linked list in an array structure.

Makes sense?

No? Only in my head? Yeah, thought so.

Ok, let me try again.

Let’s assume that we have a bunch of entries already in place. We’ll also assume there is enough space for the new entry to fit (we’ll see how free space check works in a bit).

We definitely need to maintain the key order, so we’ll scan the entries in key order - that much should be obvious.

This, in turn, means we will start the scan from the smallest_value_offset and proceed from there, following the next_pointer fields of every entry we encounter, until we find a value that is greater than the insert value (or reach the end of the list, of course).

There we insert a new entry with the appropriate next pointer, just like any linked list. We also append an index pointer at the offset value_count * size_of(u16) from the end of the file.

Note that the entry is logically inserted in the middle of the list, but physically it is appended to the end of the Entries.

If the entry is smaller than the smallest one, then we also need to update the smallest_value_offset to point to the offset of this new entry.

If the end of the list is encountered, then the next_pointer field of the entry is set to u16::MAX_VALUE to flag the end of list.

The last two cases are true at the same time for the first entry to be inserted. This, surprisingly, is not a problem and everything works out.

Size check #

New entries have to fit in the remaining space of the memtable. Remaining space can always be calculated from the write_position and value_count fields like so:

space_left_from_entries = total_size - write_position
space_left_from_pointers = space_left_from_entries - u16_bytes * value_count
space_left_from_memtable_header = space_left_from_pointers - 3 * u16_bytes
remaining_space = space_left_from_memetable_header - HEADER_SIZE - POINTER_SIZE // for the new entry

This value is passed to the KeyType::write() method, and the contract is that an error will be returned if the value does not fit in that space.

If you missed the above, don’t worry - the point is to show that all size checks can be performed with the information already present in the structure.

An example #

Let’s start from an empty memtable and insert a couple of entries in order, to see how things change.

At the beginning, the table is empty, and the various fields look like this:

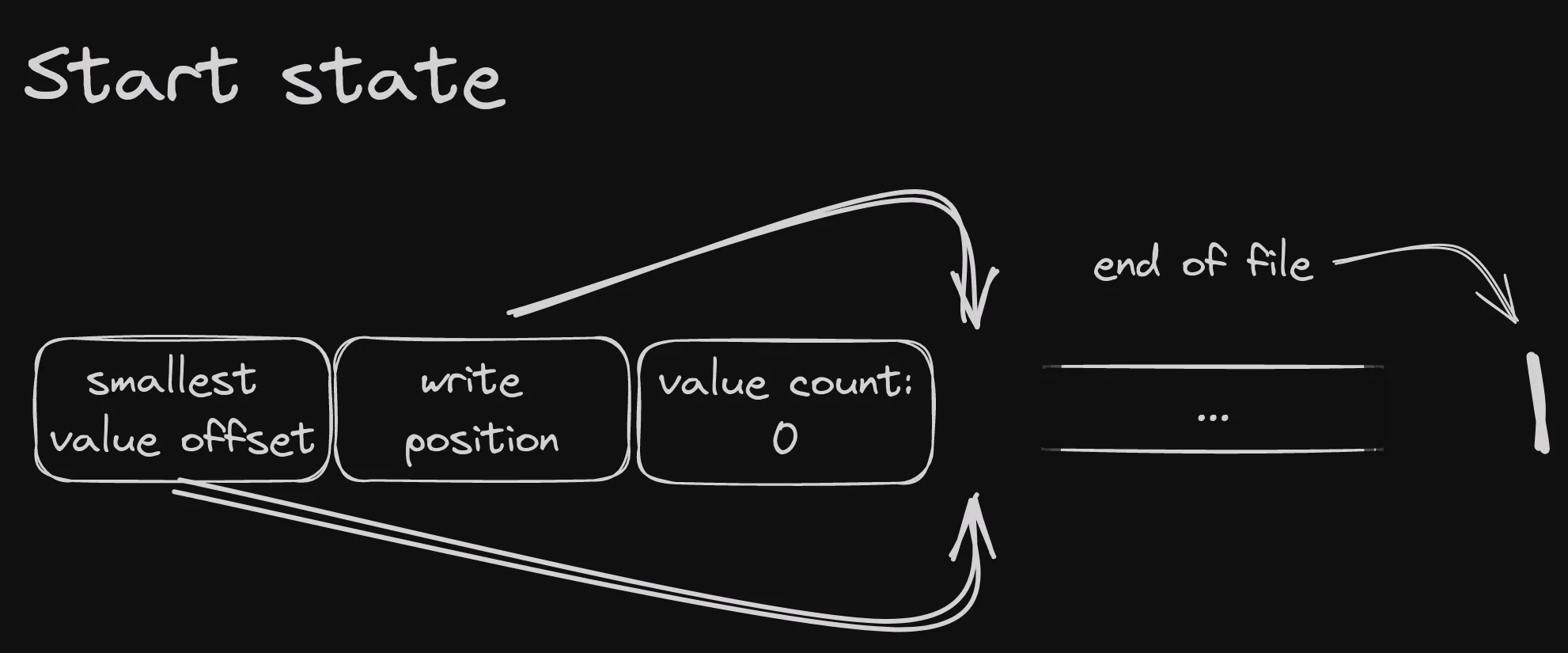
Write position is right after the memtable header, as is the smallest value offset. The value count is 0 and there are no index pointers.

After a couple of entries are inserted, it would look like this:

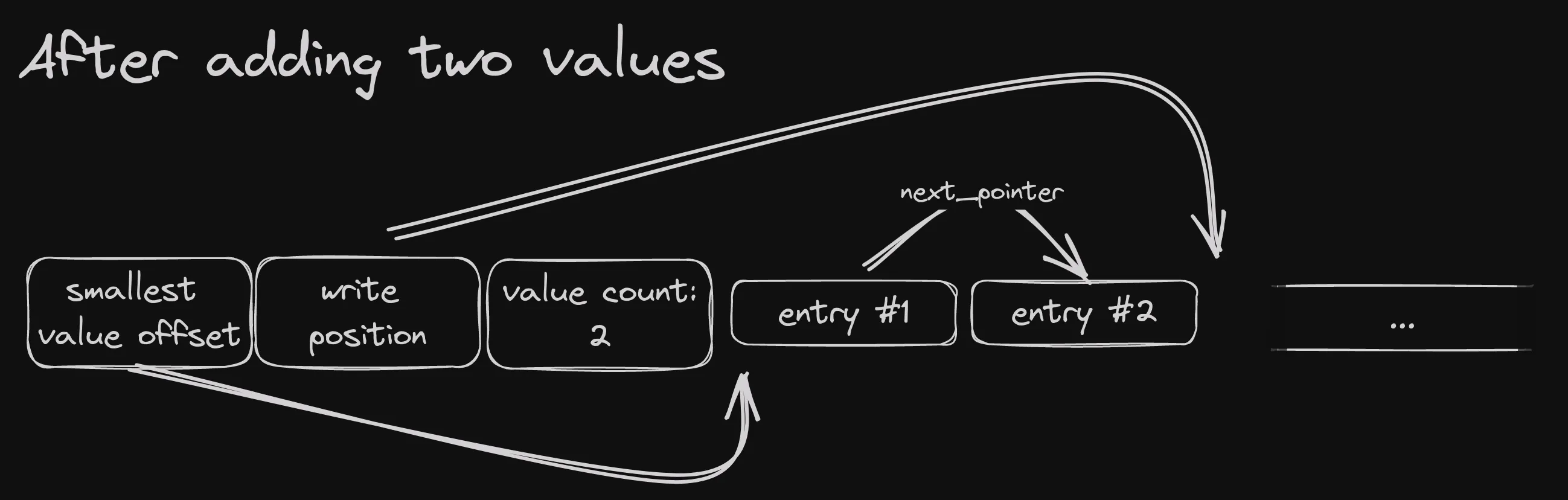
Here we assume the entries are inserted in increasing order. The smallest value offset is still pointing at the beginning of the first entry, since that’s the smallest. That, in turn, points to the next entry in order, which also happens to be right next to it. I have skipped the index pointers just to keep things tidy.

Updating an entry #

Let’s try to update an entry now - that is, add a value that is already present in the memtable.

Since we always scan in order, we are guaranteed to know if the value is already contained. In that case, we do an insert as before, in the correct place in the linked list, but we must also take care to tombstone the existing entry and have the previous linked list member point to the new entry.

Continuing the previous example, inserting a value equal to entry #2 again, it would end up looking like this:

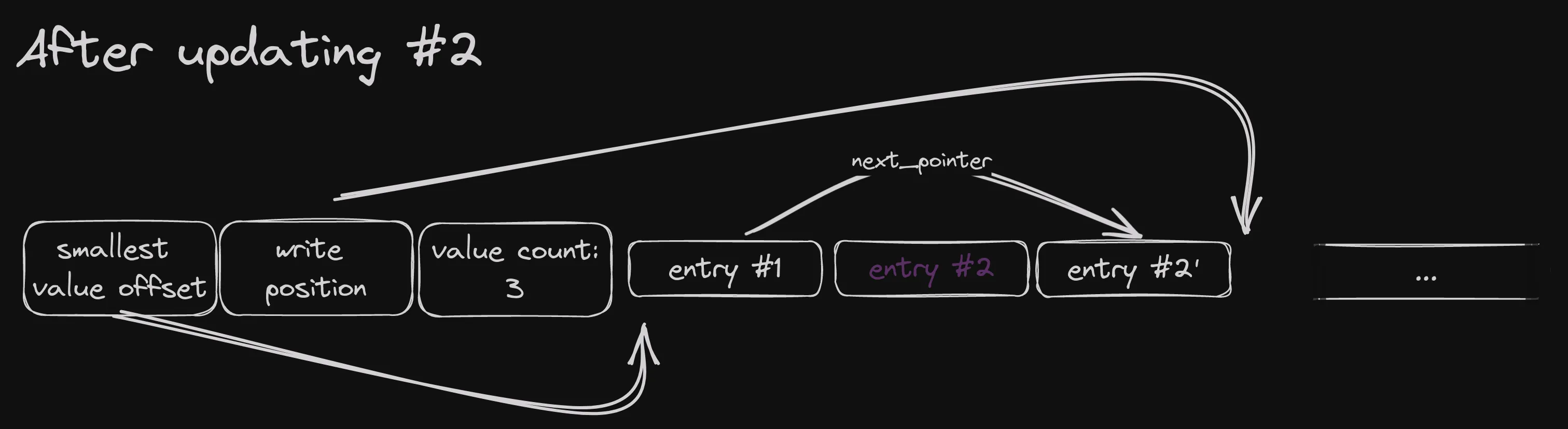
A couple of notes.

The value count increases even for updates. That’s important because we need to keep proper offsets for the index pointers. This ordered memtable, as is, doesn’t have a constant time size() function.

The original entry #2 is not removed or overwritten. Instead, it has its index field set to u16::MAX_VALUE and the next_pointer of entry #1 no longer points to it. This achieves two goals:

1. It is skipped in ordered scans of the memtable, since no previous entry points to it
2. It is skipped in linear scans, because the index field marks it as tombstoned

This makes it effectively deleted from the memtable

But wait, there’s more #

Which will have to wait for future posts, because this one is getting a bit long.

We have seen how keys are stored, which means we need to look at values next, and then how the two are combined to store pairs.

If you want to see the implementation of what I’ve described so far, you can do so in the Glowdust sources.

Of course, there is more complexity and nuance what what I’ve described here, so if you have questions or comments, drop me a line on Mastodon or open an issue and we can talk about it.

---

As always, let me know your thoughts on Mastodon

And, if you find this interesting enough, you may want to donate towards my costs as an independent developer.